Présentation de la suite de logiciels mecaflux:
Modelisation helice aerienne dans heliciel Modelisation helice bateau dans heliciel Modelisation helice ventilation dans heliciel Modelisation helice eolienne dans heliciel Modelisation hydrolienne dans heliciel Modelisation helice kaplan dans heliciel
Notion de quantité de mouvement
La quantité de mouvement d'un objet se définit comme le produit de sa masse par sa vitesse. Lorsque deux objets entrent en collision, la quantité de mouvement de chacun d'eux varie, mais la quantité de mouvement totale du système reste constante, tout au moins avec une bonne approximation.
La variation de la quantité de mouvement d'un objet est étroitement associée aux forces qui agissent sur celui-ci. Pour cette raison, on peut souvent déterminer les forces moyennes qui interviennent dans un phénomène complexe, à partir des variations de la quantité de mouvement. Les forces associées aux variations de la quantité de mouvement interviennent dans une grandeur appelée l'impulsion.
IMPULSION ET QUANTITE DE MOUVEMENT
Nous allons définir l'impulsion et la quantité de mouvement à l'aide d'un exemple. Nous établirons ensuite une relation entre ces deux grandeurs. La Fig. 7.1 montre un homme en train de pousser une armoire. Faisons l'hypothèse que les forces de frottement sur l'armoire sont négligeables. Nous pouvons établir, à l'aide des lois de Newton, une relation entre les forces qui s'exercent sur l'armoire, le temps pendant lequel les forces agissent et la variation de vitesse de l'armoire.

Supposons que la force F s'exerce sur l'armoire pendant un intervalle de temps Dt. Au cours de cet intervalle de temps, la vitesse de l'armoire varie de V0 à V2'. Par définition, l'accélération moyenne, a, est égale à la variation de vitesse divisée par l'intervalle de temps: a = (V2- V0)/Dt. La deuxième loi de Newton relie l'accélération moyenne et la force résultante F = m.a. On a donc:
ou encore: L'impulsion (newtons.secondes)se définit comme le produit de la force moyenne par l'intervalle de temps: La quantité de mouvement est définie par le produit mv, Il ressort de cette définition que l'unité de quantité de mouvement du S.I. est le kilogramme x mètre par seconde (kg .m/ s). l'impulsion est égale à la variation de la quantité de mouvement, avec P= m.V et P'= m.V'

 

lExemple: Sa masse est de 0,15 kg. Si la durée de l'impact est de 0.001 s, que vaut la force moyenne s'exerçant sur la balle?
La quantité de mouvement initiale de la balle est nulle.puisque la balle est au repos. La quantité de mouvement finale vaut P' = m.V'. A partir de la relation F.Dt= P' - P, on déduit que la force moyenne F s'exerçant sur la balle vaut:

 

CONSERVATION DE LA QUANTITE DE MOUVEMENT:  
La quantité de mouvement est une notion très utile pour étudier l'interaction entre deux ou plusieurs objets. La Fig. ci dessous schématise une collision entre deux objets. Le frottement est supposé négligeable. Chaque objet est soumis à la force de pesanteur et à une force normale.
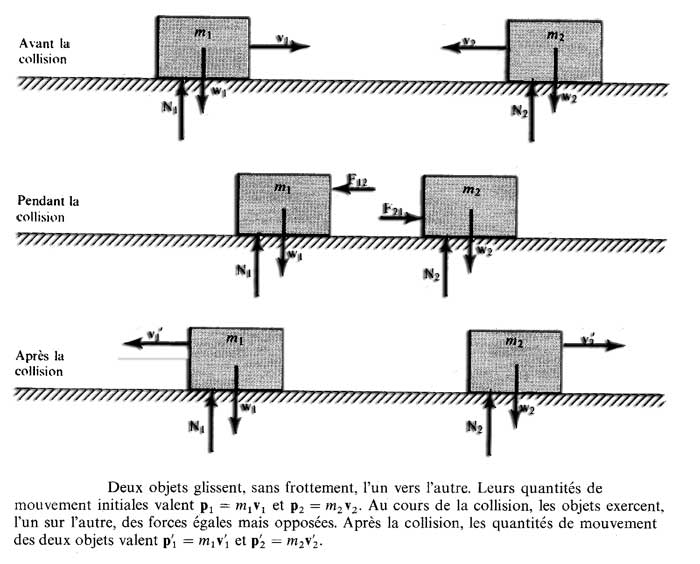Au cours de la collision, les objets exercent aussi des forces l'un sur l'autre. Ces forces F 12 et F 21 sont des forces d'action et de réaction. Elles ont donc la même grandeur, mais des directions opposées. Si la collision dure pendant un intervalle de temps Dt, la variation de la quantité de mouvement relative à chaque objet peut se calculer à partir des forces moyennes F 12 et F 21 . Comme F12 + F21 = 0, si on additionne les deux équations, on obtient et Cette équation montre que la quantité de mouvement résultante des deux objets reste inchangée avant et après la collision. La quantité de mouvement totale du système est donc conservée. Ceci est important. En effet, nous pouvons relier les vitesses des objets avant et après la collision sans rien connaître des forces qui s'exercent entre eux au cours de celle-ci. Le fait que ces forces sont égales, mais ont des directions opposées suffit à établir la relation.
Un canon est monté sur un wagon de chemin de fer. Ce wagon est initialement au repos, mais il peut se mouvoir sans frottement . On tire un boulet de canon dont la masse m vaut 5 kg et qui possède, par rapport au sol, une vitesse horizontale y = 15 m/ s. Le boulet se dirige vers la paroi du wagon. La masse totale du canon et du wagon vaut M =15.000 kg. (On suppose que la masse des gaz produits lors de l'explosion est négligeable.) (a) Que vaut la vitesse V du wagon lorsque le boulet est en vo!? (b) Si le boulet s'incruste dans la paroi du wagon, que vaut la vitesse du wagon et du boulet après l'impact?

 

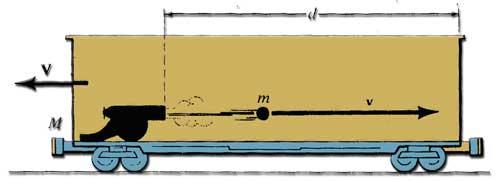
Le canon tire un boulet vers la droite. Le canon est fixé rigidement au plancher d'un wagon de chemin de fer

 

(a) Au coup de canon, le canon exerce sur le boulet une force dirigée vers la droite. Le boulet exerce une force égale mais de sens opposé sur le canon. Le canon et le wagon subissent donc un mouvement de recul vers la gauche. La quantité de mouvement totale est conservée puisqu'il n'existe aucune force externe de~ frottement. La quantité de mouvement avant le coup de canon est nulle. Dès lors, après le coup de canon, la quantité de mouvement du boulet, qui est dirigée vers la droite, doit être égale en grandeur à celle du canon et du wagon. laquelle est dirigée vers la gauche.
On a donc La vitesse de recul du canon et du wagon est très faible parce que leur masse est importante.
(b) Lorsque le boulet s'incruste dans la paroi, il exerce une force sur celle-ci. Elle est dirigée vers la droite . A son tour, la paroi exerce une force sur le boulet, qui est dirigée vers la gauche. Le boulet et le wagon cessent donc de se mouvoir. A ce moment, la quantité de mouvement résultante est à nouveau nulle. Entre-temps, le wagon s'est déplacé vers la gauche et le boulet vers la droite.